
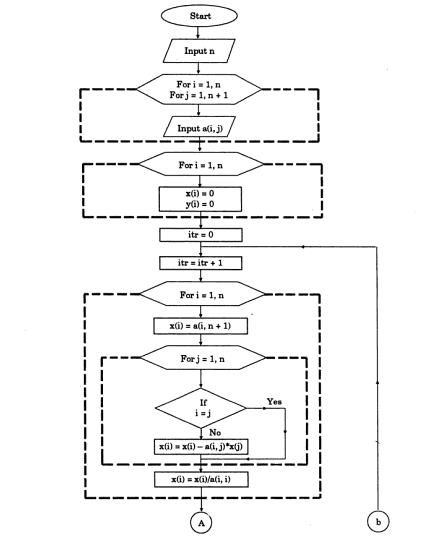
We then start with an initial guess at the potential everywhere inside the box. The way relaxation works is the following: we start with our fixed boundary condition on the outside of our simulation "box". This is our "known" starting point, and we need to then find the solutions in the middle that solve the Laplace (or the Poisson) equation. The problem we are looking at is a boundary-value problem: to be able to solve for the potential on our grid, we need to know the value of the potential on the boundaries of our simulation. Jacobi method ¶įortunately, there is a simpler method for solving these 10,000 equations, which is known as "relaxation". How many equations will we have? If we choose a grid of 100x100 points in our $x,y$ plane, we will have 10,000 equations! That's a lot! Coding this into a matrix is quite daunting. This equation is hopefully well known to you from your course in electrostatics: is is the equation that determines the electrostatic potential $\phi(\vec \approxĪll we need to do now is to equate this to zero and find the solutions of the resulting coupled (linear) equations. 13.3.We will look specifically in this course at the solutions to a specific, linear partial differential equation known as Poisson's equation: We therefore need another way of handling this type of problems. But beware, on a fairly recent Macbook Pro with \(16\) Gb of memory, the computation literally stalled when the number of grid points in both direction was multiplied by \(2\). If you want to increase the precision, you need to refine the grid. We have collected some conclusive evidence that our procedure worked very nicely! Let’s use it to assess the precision of our solution:
\ = pvec p = 0 p = 0 p = 0 p = 0 # Compute the exact solution p_e = p_exact_2d ( X, Y )Īt the beginning of the notebook, we have imported the l2_diff function from our module file module.py. Consider as an example the Poisson equation in three dimensions: This is especially true when solving multi-dimensional problems.


However, for very large systems, matrix inversion becomes an expensive operation in terms of computational time and memory. When the size of the matrix is not too large, one can rely on efficient direct solvers. Their implementation is a bit more complicated in the sense that they require the inversion of a matrix.
In the previous chapter we have discussed how to discretize two examples of partial differential equations: the one dimensional first order wave equation and the heat equation.įor the heat equation, the stability criteria requires a strong restriction on the time step and implicit methods offer a significant reduction in computational cost compared to explicit methods. insert ( 0, './modules' ) # Function to compute an error in L2 norm from norms import l2_diff % matplotlib inline Import numpy as np import matplotlib.pyplot as plt from scipy.sparse import diags import sys sys.


 0 kommentar(er)
0 kommentar(er)
